LA Namespace Reference

Functions
std::vector< double >	ROOTEquationSolver (const double &m1, const double &b1, const double &m2, const double &b2, const double &m3, const double &b3, bool debugMode)
void	GaussianElimination (std::vector< std::vector< double >> &mat, bool debugMode=false)
int	GetMatrixRank (const std::vector< std::vector< double >> &mat)
int	CheckSolutions (const std::vector< std::vector< double >> &mat, std::vector< double > &solution)
bool	ValidateSolution (const std::vector< std::vector< double >> &origMat, const std::vector< double > &solution, bool debugMode)
bool	IsSlopeUndefined (double slope)
std::vector< double >	SolveSystemOfThreeEquations (const double &m1, const double &b1, const double &m2, const double &b2, const double &m3, const double &b3, bool debugMode)

Function Documentation

CheckSolutions()

int LA::CheckSolutions	(	const std::vector< std::vector< double >> &	mat,
		std::vector< double > &	solution
	)

Function to check the type of solution

Create the augmented matrix by copying the original matrix and adding a column of constants

Remove the solution column to get the coefficient matrix

No solution

Infinite solutions

Perform back substitution to find the solution

No solution

Unique solution

Here is the call graph for this function:

Here is the caller graph for this function:

GaussianElimination()

void LA::GaussianElimination	(	std::vector< std::vector< double >> &	mat,
		bool	debugMode = false
	)

Function to perform Gaussian elimination. converts the matrix to an upper triangular form.

Find pivot for column i

If the pivot is zero, skip this column

Scale pivot row

Eliminate below

Here is the call graph for this function:

Here is the caller graph for this function:

GetMatrixRank()

int LA::GetMatrixRank

(

const std::vector< std::vector< double >> &

mat

)

Function to determine the rank of the matrix

Here is the caller graph for this function:

IsSlopeUndefined()

bool LA::IsSlopeUndefined

(

double

slope

)

A helper function to check if a slope is undefined.

ROOTEquationSolver()

std::vector<double> LA::ROOTEquationSolver	(	const double &	m1,
		const double &	b1,
		const double &	m2,
		const double &	b2,
		const double &	m3,
		const double &	b3,
		bool	debugMode
	)

uses TDecompSVD, which performs a singular value decomposition to solve the linear system

Solution vector

Solve the system

Handle the error by returning an empty vector.

If is_good_solution is true, convert solution into an std::vector and return it.

Parameters

m2	XZ projection: z = m1*x + b1
m3	YZ projection: z = m2*y + b2
debugMode	XY projection: y = m3*x + b3

Here is the call graph for this function:

Here is the caller graph for this function:

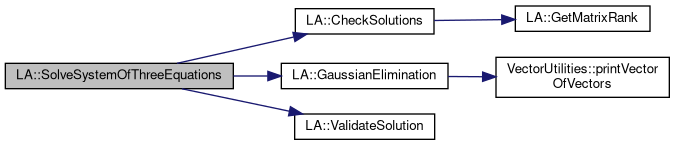
SolveSystemOfThreeEquations()

std::vector<double> LA::SolveSystemOfThreeEquations	(	const double &	m1,
		const double &	b1,
		const double &	m2,
		const double &	b2,
		const double &	m3,
		const double &	b3,
		bool	debugMode
	)

To solve Augmented matrix representation of the system of equations Form: ax + by + cz = d

Parameters

m2	XZ projection: z = m1*x + b1
m3	YZ projection: z = m2*y + b2
debugMode	XY projection: y = m3*x + b3

Here is the call graph for this function:

Here is the caller graph for this function:

ValidateSolution()

bool LA::ValidateSolution	(	const std::vector< std::vector< double >> &	origMat,
		const std::vector< double > &	solution,
		bool	debugMode
	)

The solution does not satisfy the equation

The solution satisfies all equations

Here is the caller graph for this function: